Chronos-2: Cold-Start Forecasting with Short Histories and No Training — A Practical Tutorial

An interesting case with the Chronos-2 foundation model

Cold-start forecasting example where Series 1 has a shorter context length. Enabling in-context learning (bottom) improves performance compared with univariate forecasting (top) (Image by author, Source)

In this follow-up article, we explore an interesting challenge:

How can we use the foundation model Chronos-2 in a cold-start forecasting scenario — where we have a collection of interdependent time series, but some of them have only short histories?

Consider a retail forecasting example: a new product is introduced, but little contextual data is available for training—let alone for inference.

Fortunately, Chronos-2 requires no additional training. Moreover, when a product has only a brief historical record, Chronos-2’s in-context learning capability allows it to leverage information from other similar series in the dataset.

By using in-context learning, Chronos-2 effectively leverages patterns from related time series to improve predictions for those with limited history.

Let’s walk through a cold-start forecasting example with Chronos-2 below.

✅ Find the notebook for this article here: AI Projects Folder (Project 27)

Cold-Start Forecasting with Chronos-2

We’ll simulate a cold-start forecasting scenario by reducing the historical context for one of the time series while keeping full history for the others. This mimics cases like new product launches, where only a short history is available.

We’ll use the Kaggle Tabular Competition dataset. For details on downloading and preparing the dataset, check my previous article:

Chronos-2: Zeroshot Multivariate Forecasting with Covariates — A Practical Tutorial for Retail Forecasting

We’ll also rely on the helper functions split_train_test(), plot_timeseries(), and chronos_forecast()—all of which are available in the accompanying notebook.

In the dataframe Y_train_df_cold shown below, every time series has a maximum context_length = 1300, except for the first time-series ID, “Belgium_KaggleMart_Kaggle Advanced Techniques”, whose context length is roughly half (about 600). This setup simulates a cold-start scenario.

Below, we run 2 experiments:

1. Univariate + Covariates (calendar-based features): Each time series is forecast independently.

2. Multivariate + Covariates with “cross_learning = True”: All time series share information and are forecast jointly.

In the 1st case, the model is expected to struggle with the shorter time series because it lacks access to the full context length.

In the 2nd case, Chronos-2 considers global interdependencies among all time series of the dataset, and in-context learning should compensate for the reduced context length, producing more accurate forecasts.

context_length=1300
prediction_length=24
num_windows = 1
TEST = prediction_length * num_windows
item_list = df[’unique_id’].unique().tolist()
quantile_levels = [i/10 for i in range(1, 10)]

target_id = ‘Belgium_KaggleMart_Kaggle Advanced Techniques’
Y_train_df, Y_test_df = split_train_test(df, context_length, TEST)

# Cold-start modification only for the target_id, the first slash_n datapoints will be dropped
def modify_cold_start(Y_train_df, target_id, slash_n=700, context_length=1300):

    target_df = Y_train_df[Y_train_df[’unique_id’] == target_id]
    other_df  = Y_train_df[Y_train_df[’unique_id’] != target_id]

    target_df = target_df.sort_values(’ds’).iloc[slash_n:]
    target_df = target_df.tail(context_length)
    out = (
        pd.concat([other_df, target_df], axis=0)
        .sort_values([’unique_id’, ‘ds’])
        .reset_index(drop=True)
    )
    return out

Y_train_df_cold = modify_cold_start(Y_train_df, target_id)

Let’s view the first case, univariate forecasting.

No Cross-learning: Univariate Forecasting + Covariates

Let’s see what happens when Chronos-2 uses:

• The full context lengths (Y_train_df).

• The first time series of the dataset has a shorter context length, while the others use the maximum context length (Y_train_df_cold).

The plot_timeseries() function below plots the first 2 time series of the dataset (notice the n_series_to_plot=2), but the dataset has 48 time series (products) in total.

cols = [”day”,”month”,”is_holiday”,”country”,”store”,”product”,”holiday_name”]
quantiles, mean, inputs, actuals = chronos_forecast(Y_train_df, Y_test_df, item_list,  prediction_length=prediction_length, quantile_levels=quantile_levels, covariates=cols, cross_learning=False)
inputs_f = [v[”target”] for v in inputs]
actuals_f = [v[”target”] for v in actuals]

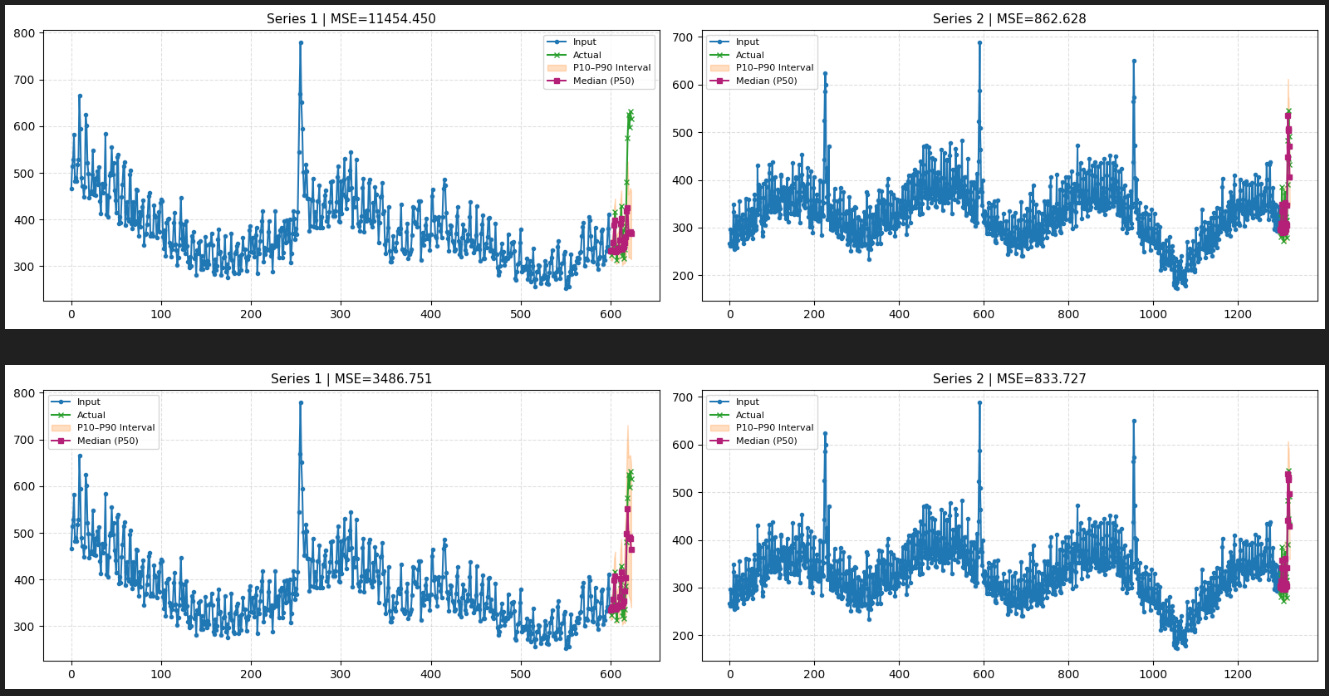
df_mse = plot_timeseries(inputs_f, quantiles, actuals_f, n_series_to_plot=2,intervals=True)
print(f”Mean MSE of Chronos over all time-series: {df_mse[”mse”].mean()}”)

print(f”\n\n----- Forecasting with {target_id} having a shorter context-length\n\n”)

quantiles, mean, inputs, actuals = chronos_forecast(Y_train_df_cold, Y_test_df, item_list,  prediction_length=prediction_length, quantile_levels=quantile_levels, covariates=cols, cross_learning=False)
inputs_f = [v[”target”] for v in inputs]
actuals_f = [v[”target”] for v in actuals]
df_mse = plot_timeseries(inputs_f, quantiles, actuals_f, n_series_to_plot=2,intervals=True)
print(f”Mean MSE of Chronos over all time-series: {df_mse[”mse”].mean()}”)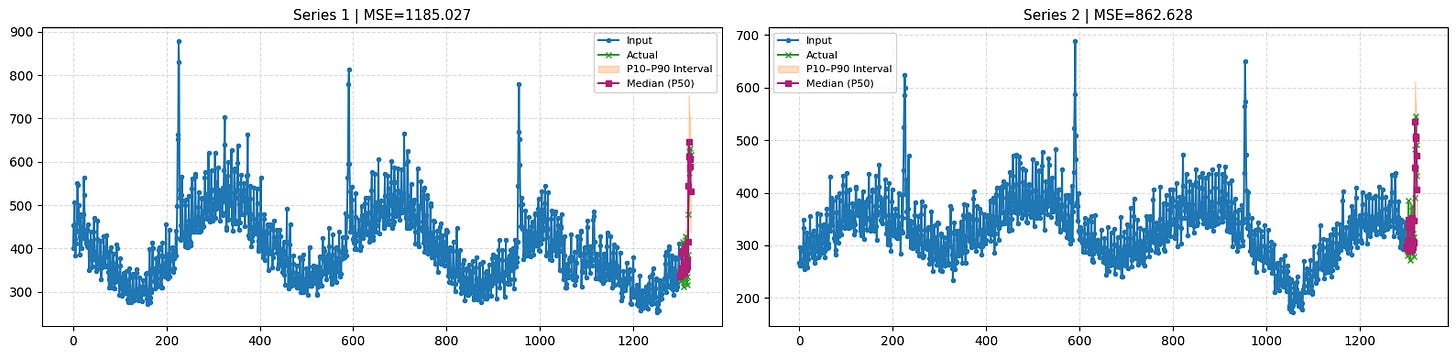

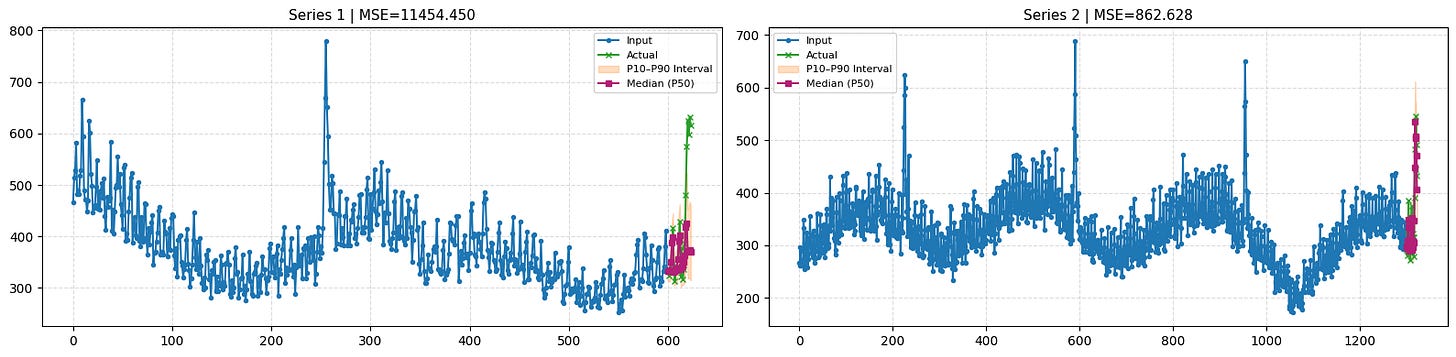
Figure 1: Predictions using the Y_train_df dataset (Image by author, Source)

Figure 2: Predictions using the Y_train_df_cold dataset. Only the first time series has a shorter context length than the others (Image by author, Source)

The 1st time series in Figure 1 looks as expected, since the full context is used. However, in Figure 2, which simulates a cold-start scenario for that same series, we notice an issue:

Without cross-learning, the model fails to capture the final peak of the short time series, since each series is modeled independently.

The 90th percentile forecast also misses this final peak.

Therefore, the first peak within the available context window is interpreted as an anomaly and is ignored by the model.

With Cross-learning: Multivariate Forecasting + Covariates

Let’s see what happens if we enable cross-learning (essentially multivariate forecasting). We only set cross_learning=True:

quantiles, mean, inputs, actuals = chronos_forecast(Y_train_df_cold, Y_test_df, item_list,  prediction_length=prediction_length, quantile_levels=quantile_levels, covariates=cols, cross_learning=True)
inputs_f = [v[”target”] for v in inputs]
actuals_f = [v[”target”] for v in actuals]
df_mse = plot_timeseries(inputs_f, quantiles, actuals_f, n_series_to_plot=2,intervals=True)
print(f”Mean MSE of Chronos over all time-series: {df_mse[”mse”].mean()}”)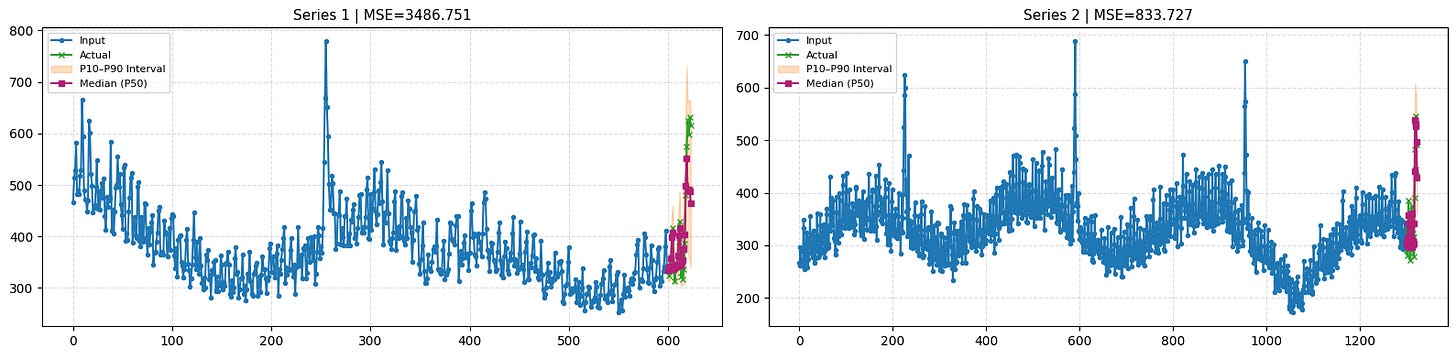

Figure 3: Predictions using the Y_train_df_cold dataset, with cross_learning=True enabled (Image by author, Source)

With cross-learning enabled and joint predictions across all time series, the model performs noticeably better on the short series.

Although it does not fully capture the final peak, the 90th percentile interval does account for it.

The model still cannot decisively determine whether the first peak is an anomaly, but by learning from the other series in the dataset, it adjusts its prediction intervals to more accurately represent the underlying uncertainty!

---

Thank you for reading!

Horizon AI Forecast is a reader-supported newsletter, featuring occasional bonus posts for supporters. Your support through a paid subscription would be greatly appreciated.

---

References

[1] Ansari et al. Chronos-2: From Univariate to Universal Forecasting

[2] Kaggle Tabular Playground Series - Sep 2022