MOIRAI-MOE : Upgrading MOIRAI with Mixture-of-Experts for Enhanced Time Series Forecasting
The popular foundation time-series model just got an update!
The race to build the Top foundation forecasting model is on!
Salesforce’s MOIRAI, one of the early foundation models — achieved high benchmark results and was open-sourced along with its pretraining dataset, LOTSA.
We extensively analyzed how MOIRAI works here — and built an end-to-end project comparing MOIRAI with popular statistical models here.
Salesforce has now released an upgraded version—MOIRAI-MOE—with significant improvements, particularly the addition of Mixture-of-Experts (MOE). We briefly discussed MOE when another model, Time-MOE, also used multiple experts.
In this article, we’ll cover:
How MOIRAI-MOE works and why it’s a powerful model.
Key differences between MOIRAI and MOIRAI-MOE.
How MOIRAI-MOE’s use of Mixture-of-Experts enhances accuracy.
How Mixture-of-Experts generally solves frequency variation issues in foundation time-series models.
Let’s get started.
✅ Horizon AI Forecast is a reader-supported newsletter, featuring occasional bonus posts for supporters. Your support through a paid subscription would be greatly appreciated.
MOIRAI vs MOIRAI-MOE
MOIRAI-MOE is a Decoder-only, Foundation time-series model using Mixture-of-Experts to perform generalizable, frequency-invariant forecasting with fewer parameters.
A comparison between the two models (original MOIRAI vs. MOIRAI-MOE) is shown in Figure 1:

Let’s break down these differences:
1. MOIRAI-MOE is now a Decoder-only model
MOIRAI-MOE departs from MOIRAI’s original masked encoder architecture, adopting a decoder-only setup.
Decoder-only Transformers enable fast parallel training, processing multiple training examples with varying context lengths in a single update. However, an Encoder offers faster inference, as it can perform multi-step predictions in one forward pass. In contrast, decoder-only Transformers and RNNs must make predictions autoregressively, requiring multiple forward passes for multi-step forecasts.
This isn’t an issue for MOIRAI-MOE, as the sparse Mixture-of-Experts (MOE) architecture lets it activate fewer parameters—outperforming the dense MOIRAI. In an experiment comparing MOIRAI, MOIRAI-MOE, and Chronos, all with the same context lengths, MOIRAI-MOE achieves the faster inference:

MOIRAI-MOE-Base, while 3x larger than MOIRAI-Large, activates only 86M params with MOE — running significantly faster than MOIRAI-Large (370 seconds vs. 537).
Moreover, encoders are better suited for models integrating future-known variables—a feature unique to the original MOIRAI. It’s unclear if the Decoder-only architecture can support future-known variables, so I’ll have to check the code once released.
Of course, past covariates can be used—MOIRAI-MOE uses them similarly to MOIRAI.
2. Replacing the Multi-Patch Layer with Mixture-of-Experts
The original MOIRAI model used Multi-Patch Layers to handle varying frequencies by learning specific patch sizes for each granularity.
As we discussed in Time-MOE, Mixture-of-Experts (MOE) replaces an overparameterized dense FFN with a sparse layer, where a gating function assigns each input to the expert (an FNN) with the highest score.
Handling diverse frequencies is crucial for any foundational time-series model. MOIRAI addressed this by using Multi-Patch Layers that project the input to different patch lengths based on the dataset frequency specified by the user.

In my original MOIRAI article, I noted that Multi-Patch Layers somewhat mimic Mixture-of-Experts. Now, MOIRAI-MOE replaces the Multi-Patch Layers with a single projection layer and uses the MOE mechanism to handle multiple frequencies.
But why isn’t the original MOIRAI’s Multi-Patch Layer enough, and why does Mixture-of-Experts handle different frequencies better?
Because time-series data often contains diverse sub-frequencies. Also, time series with different frequencies can share patterns, while those with the same frequency may not. Therefore, labeling data with an arbitrary frequency is sometimes flawed (Figure 4):

Thus Mixture-of-Experts improves MOIRAI in the following way:
Users no longer need to specify a frequency parameter for MOIRAI.
MOE routes time sequences to the best-suited expert, based on data-driven routing.
By using Mixture-of-Experts, MOIRAI-MOE moves beyond manual frequency heuristics, learning instead to assign time series to the right expert autonomously.
In fact, MOIRAI-MOE introduces an enhanced MOE mechanism tailored for time-series forecasting. We’ll explore this in the next section.
3. Different Attention Mechanism
With its decoder-only architecture, MOIRAI-MOE switches from an any-variate attention mechanism to causal self-attention, similar to GPT models.
It’s unclear if the new model retains LLM features like ROPE, SwiGLU activations, or RMSNorm—we’ll know when the code is released.
However, the model’s output remains unchanged: MOIRAI-MOE doesn’t directly forecast timepoints but instead predicts parameters of a mixture distribution, which is then sampled to generate forecasts. The learning objective is the same, minimizing the negative log-likelihood of the mixture distribution.
Hence, MOIRAI-MOE is a probabilistic model. Enhanced uncertainty quantification, like conformalized quantile regression, could be added to produce prediction intervals (since MOIRAI-MOE can produce quantile predictions)
Enter MOIRAI-MOE
This work introduces two new MOIRAI-MOE variants, detailed in Figure 5:

MOIRAI-MOE-base is 3 times larger than MOIRAI-large — but uses the same number of parameters for inference thanks to the MOE mechanism.
In short, MOIRAI-MOE replaces fully-connected layers with a sparse Mixture of Experts layer. This layer includes a gating function that calculates scores, routing input to the top K experts based on these scores
Figure 5 shows that MOIRAI-MOE uses 32 experts in total, with the top 2 (TopK=2) activated per input:

Moreover, MOIRAI-MOE takes it a step further and replaces the linear projection W above with a more sophisticated mechanism:
The authors used the self-attention weights of the pretrained MOIRAI model to do K-Means clustering, with number_of_clusters = M (the total number of experts).
Thus we calculate M cluster centroids, 1 per Expert.
During training, instead of learning the gating function from scratch (the linear projection W in equation 1), the MOIRAI-MOE assigns the input to the Expert which scores the lowest Euclidean distance between the input and that Expert’s cluster centroid.
Thus, the gating equation becomes as follows:

where x is the input to the MOE layer l and C the cluster centroids.
Using this token-cluster approach yields superior results in benchmarks (Figure 6):

The authors observed that the centroids capture well-structured data patterns, enhancing routing accuracy and boosting performance. Figure 6 also shows that the decoder-only architecture outperforms MOIRAI’s original encoder-only setup.
The Impact of Mixture-of-Experts in a Time-Series Model
Adding MOE to MOIRAI yields improved results. But what do the Experts learn, and how do they handle different frequencies?
The authors analyzed the distribution of Expert activations in each layer, focusing on different frequencies. Figure 7 shows the results:

Let’s analyze the findings:
The x-axis shows the Expert index (32 total), and the y-axis shows the percentage of tokens routed to each expert.
In the initial layers, Expert selection is diverse — with different expert allocations for different frequencies.
However, as tokens pass through the deeper layers, the model shifts its focus to general temporal characteristics—such as trends and seasonality—typical of time series, regardless of frequency.
In contrast, LLMs that use MOE display the reverse pattern: Initial layers activate a small percentage of experts, while deeper layers show greater diversity.
This inverted pattern in time-series models may be due to the noisier, dynamic nature of time-series data, generated from limited windows (patches), unlike NLP tokens, which stem from a fixed vocabulary and are more predictable.
Certain experts are rarely activated, suggesting that pruning them may be considered in future work.
Therefore we can conclude:
Mixture-of-Experts in a time-series foundation model is a hierarchical denoising process — where the first Expert layers focus on frequency-related characteristics and deeper layers target broader patterns — like long-term trends and seasonalities.
Evaluating MOIRAI-MOE
Finally, the authors pretrained MOIRAI-MOE on the same dataset as MOIRAI—LOTSA, a dataset with 27B observations across 9 domains.
They used patch_size =16 (this value was found experimentally). The small and base versions were trained for 50k and 250k epochs respectively. No large version was created this time (no need since MOIRAI-MOE-base is equivalent to MOIRAI-large).
Like MOIRAI, MOIRAI-MOE was evaluated in 2 scenarios:
Out-of-distribution forecasting(zero-shot): The model performs zero-shot forecasts on unseen datasets excluded from LOTSA, — competing against other SOTA models specifically trained on these datasets.
In-distribution forecasting: The model is fine-tuned on LOTSA training subsets and evaluated on their test subsets.
Testing was rigorous:
Non-foundation models were fully tuned, and testing followed a rolling forecasting scenario. The test set contained the last h×r time steps (where h is the forecast horizon and r is the number of rolling evaluation windows).
The validation set is the forecast horizon just before the test set, and the benchmarks present the best-tuned model with the lowest CRPS on validation data. CRPS is a proper score metric.
The in-distribution datasets contain datasets with different frequencies — to make the test thorough.
The zero-shot and in-distribution benchmarks are displayed in Figures 8 and 9:

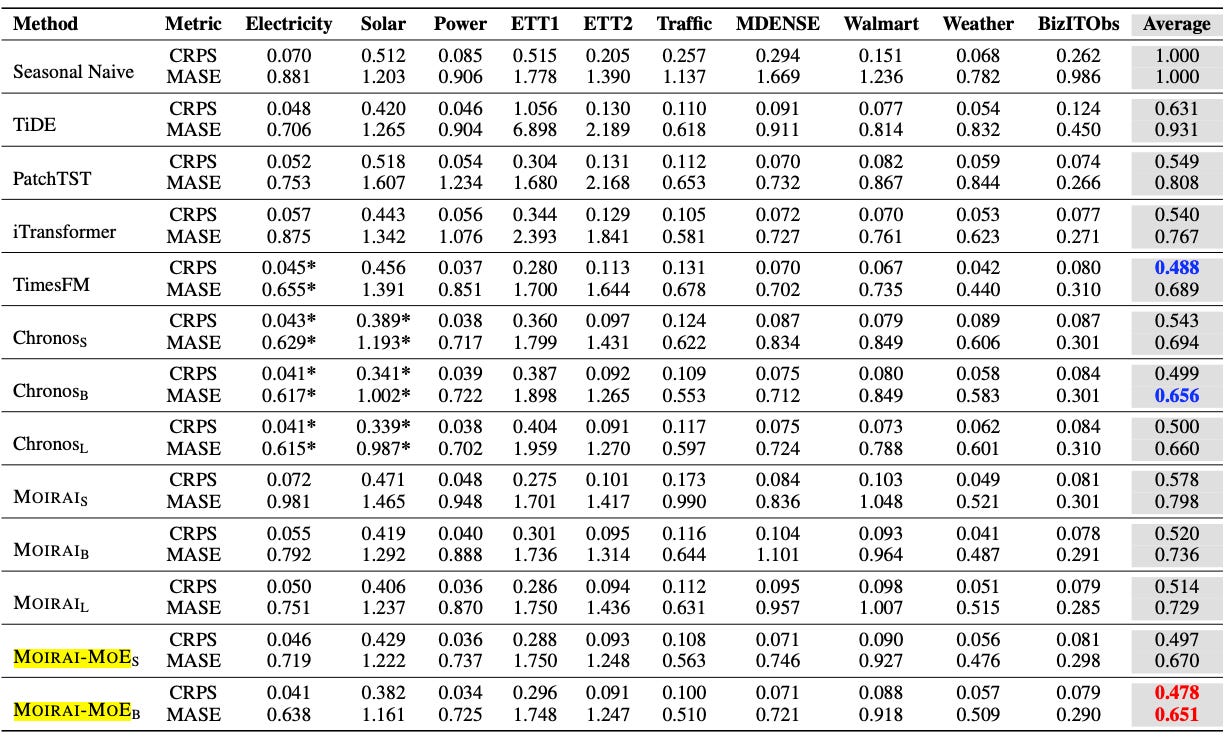
In the zero-shot benchmark, MOIRAI-MOE-Base achieves the best overall score - outperforming both foundation and fully-trained models
The same benchmark also revealed that foundation models generally perform better on average than other models (Statistical, ML, DL).
In the full-shot benchmark, MOIRAI-MOE-Base again secured the top position, followed by TimesFM (CRPS) and Chronos (MASE).
MOIRAI-MOE surpasses the original MOIRAI in both benchmarks, delivering 17% better performance with 65X fewer activated parameters.
Notice that some foundation models are marked with asterisks on specific datasets - indicating that those datasets were included in their pretraining corpora.
Unfortunately, Tiny Time Mixers, a powerful MLP-based foundation forecasting model, is absent from the benchmark.
Overall, the results are highly encouraging. While many foundation models avoid benchmarking against fully-tuned models, MOIRAI-MOE confidently outperforms them.
Closing Remarks
MOIRAI-MOE is a milestone in foundation models, achieving impressive results over its predecessor.
More importantly, the pace at which foundation models improve is remarkable, especially with the open-sourcing of models and their pretraining datasets.
Until 2 years ago, Monash was the only open repository for diverse, quality time-series datasets. That is no longer the case.
Finally, Mixture-of-Experts is a well-established ML technique, and its entry into the time-series foundation space paves the way for further advancements. We previously discussed Time-MOE, and more models are expected to adopt MOE.
Thank you for reading!
Horizon AI Forecast is a reader-supported newsletter, featuring occasional bonus posts for supporters. Your support through a paid subscription would be greatly appreciated.
References
Liu et al. MOIRAI-MOE: Empowering Time Series Foundation Models With Sparse Mixture Of Experts
Woo et al., Unified Training of Universal Time Series Forecasting Transformers(February 2024)


